Dekompressionsberechnung mit Mischgasen
Geht Helium als weiteres Inertgas in die Sättigungsrechnung mit ein, so verhalten sich die Gewebeinertgasdrücke für Helium und Stickstoff additiv s. Gl. (30) ([1], S. 101 ff.)
 |
(30) |
In Gl. (31) wird gezeigt, wie sich Gl. (30) auf die Sättigungsgleichung (1) auswirkt:
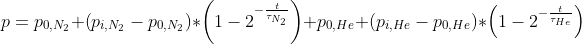 |
(31) |
Um nun bei Verwendung von Mischgasen die Zeit zu berechnen, die auf einer Dekostufe verbracht werden muss, bevor zur nächsten Stufe aufgestiegen werden kann, ziehen wir wieder Gl. (10) heran und betrachten die einzelnen Terme in Bezug auf mehrere Inertgase.
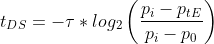 |
(10)
|
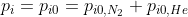 |
(32)
|
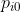 ist der inspiratorische, resp. alveolare Inertgasdruck zu Beginn der Dekompression auf der aktuellen Stufe und für jedes Inertgas separat wie in Gl. (2) - Gl. (4) berechnet. ist der inspiratorische, resp. alveolare Inertgasdruck zu Beginn der Dekompression auf der aktuellen Stufe und für jedes Inertgas separat wie in Gl. (2) - Gl. (4) berechnet. 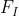 ist dabei derAnteil des jeweiligen Inertgases. ist dabei derAnteil des jeweiligen Inertgases.
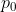 ist der Gewebeinertgasdruck im jeweiligen Kompartiment zu Beginn der Dekompression auf der aktuellen Stufe. Hier ist wieder zu beachten, dass dieser sich aus der Summe aller verwendeten Gewebeinertgasdrücke zusammensetzt (Gesetzt von Dalton). Dabei gilt analog Gl. (30). ist der Gewebeinertgasdruck im jeweiligen Kompartiment zu Beginn der Dekompression auf der aktuellen Stufe. Hier ist wieder zu beachten, dass dieser sich aus der Summe aller verwendeten Gewebeinertgasdrücke zusammensetzt (Gesetzt von Dalton). Dabei gilt analog Gl. (30).
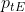 ist der Gewebeinertgasdruck am Ende der notwendigen Dekompression (also am Ende des notwendigen Expositionszeitraums) auf der aktuellen Stufe und wird ähnlich Gl. (11) für jedes Kompartiment berechnet (s. Gl. 33) ist der Gewebeinertgasdruck am Ende der notwendigen Dekompression (also am Ende des notwendigen Expositionszeitraums) auf der aktuellen Stufe und wird ähnlich Gl. (11) für jedes Kompartiment berechnet (s. Gl. 33)
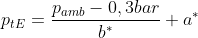 |
(33) |
![a^*=a(N_2+ He)=\left [ (P_{N_2}*a_{N_2})+(P_{He}*a_{He}) \right ]/(P_{N_2} + P_{He}) a^*=a(N_2+ He)=\left [ (P_{N_2}*a_{N_2})+(P_{He}*a_{He}) \right ]/(P_{N_2} + P_{He})](http://latex.codecogs.com/gif.latex?a%5E%2A%3Da%28N_2%2B%20He%29%3D%5Cleft%20%5B%20%28P_%7BN_2%7D%2Aa_%7BN_2%7D%29%2B%28P_%7BHe%7D%2Aa_%7BHe%7D%29%20%5Cright%20%5D%2F%28P_%7BN_2%7D%20%2B%20P_%7BHe%7D%29) |
(34) |
![b^*= b(N_2+ He)=\left [ (P_{N_2}*b_{N_2})+(P_{He}*b_{He}) \right ]/(P_{N_2} + P_{He}) b^*= b(N_2+ He)=\left [ (P_{N_2}*b_{N_2})+(P_{He}*b_{He}) \right ]/(P_{N_2} + P_{He})](http://latex.codecogs.com/gif.latex?b%5E%2A%3D%20b%28N_2%2B%20He%29%3D%5Cleft%20%5B%20%28P_%7BN_2%7D%2Ab_%7BN_2%7D%29%2B%28P_%7BHe%7D%2Ab_%7BHe%7D%29%20%5Cright%20%5D%2F%28P_%7BN_2%7D%20%2B%20P_%7BHe%7D%29) |
(35) |
![\tau^*=\tau(N_2 + He)=\left [ (P_{N_2}*\tau_{N_2})+(P_{He}*\tau_{He}) \right ]/(P_{N_2} + P_{He}) \tau^*=\tau(N_2 + He)=\left [ (P_{N_2}*\tau_{N_2})+(P_{He}*\tau_{He}) \right ]/(P_{N_2} + P_{He})](http://latex.codecogs.com/gif.latex?%5Ctau%5E%2A%3D%5Ctau%28N_2%20%2B%20He%29%3D%5Cleft%20%5B%20%28P_%7BN_2%7D%2A%5Ctau_%7BN_2%7D%29%2B%28P_%7BHe%7D%2A%5Ctau_%7BHe%7D%29%20%5Cright%20%5D%2F%28P_%7BN_2%7D%20%2B%20P_%7BHe%7D%29) |
(36) |
Die Sache hat nun einen Haken: 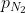 und und 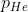 aus Gl. (34) - (35) sind die jeweiligen Gewebeinertgasdrücke am Ende der Dekostufe. Nun geht es hier aber darum, die Verweildauer auf dieser Dekostofe erst zu ermitteln. aus Gl. (34) - (35) sind die jeweiligen Gewebeinertgasdrücke am Ende der Dekostufe. Nun geht es hier aber darum, die Verweildauer auf dieser Dekostofe erst zu ermitteln. 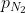 und und 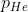 sind daher zwei Unbekannte und damit gilt das ebenfalls für sind daher zwei Unbekannte und damit gilt das ebenfalls für 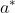 und und 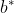 . .
Es gibt verschiedene Möglichkeiten, dieses Dilemma zu lösen ([5], "Mischgas Theorie").
Bei der "numerischen Methode" wird so vorgegangen, dass ausgehend vom Zeitpunkt 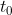 kleine Zeitschritte kleine Zeitschritte 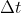 addiert werden.Das Ziel ist erreicht, wenn das Ergebnis addiert werden.Das Ziel ist erreicht, wenn das Ergebnis 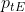 kleiner oder gleich dem tolerierten Gewebeinertgasdruck der Zieldekostufe ist. kleiner oder gleich dem tolerierten Gewebeinertgasdruck der Zieldekostufe ist.
Formal sieht das so aus:
 |
(37) |
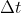 ist eine kleine Zeiteinheit, z. B. >= 1 sec. Aufgrund des immensen Rechenaufwandes kann ist eine kleine Zeiteinheit, z. B. >= 1 sec. Aufgrund des immensen Rechenaufwandes kann 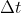 aber auch größer gewählt werden, z. B. 1 Minute, wenn als Regel gewählt wird, dass mindestens eine Minute auf jeder Dekostufe verblieben werden muss. aber auch größer gewählt werden, z. B. 1 Minute, wenn als Regel gewählt wird, dass mindestens eine Minute auf jeder Dekostufe verblieben werden muss.
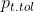 ist der tolerierte Gewebeinertgasüberdruck auf der nächst niedrigeren Dekostufe (in der Regel 3 m flacher). Für die Berechnung wird der Umgebungsdruck auf der nächst niedrigeren Dekostufe herangezogen (s. Gl. (38)) ist der tolerierte Gewebeinertgasüberdruck auf der nächst niedrigeren Dekostufe (in der Regel 3 m flacher). Für die Berechnung wird der Umgebungsdruck auf der nächst niedrigeren Dekostufe herangezogen (s. Gl. (38))
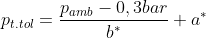 |
(38) |
Für die Berechnung von 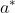 und und 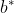 werden selbstverständlich die jeweils aktuellen Zwischenstufen von werden selbstverständlich die jeweils aktuellen Zwischenstufen von  herangezogen. herangezogen.
In Abbildung 1 wird das "Absitzen" auf Dekostufen grafisch dargestellt.

Abbildung 1, Gewebeinertgasdruck auf den Dekostufen
Punkt 1) kennzeichnet 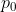 als neue Ausgangsbasis für die Berechnung von 2) als neue Ausgangsbasis für die Berechnung von 2) 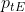 . Das wiederum wird verglichen mit . Das wiederum wird verglichen mit 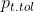 , dem tolerierten Gewebeinertgasdruck in Punkt 3), in diesem Beispiel also drei Meter höher. , dem tolerierten Gewebeinertgasdruck in Punkt 3), in diesem Beispiel also drei Meter höher.
Alternativ zu dem oben geschilderten Vorgehen kann aus dem aktuellen Gewebeinertgasdruck auch der tolerierte Umgebungsdruck ermittelt werden. Es wird solange auf der aktuellen Dekostufe verblieben, bis durch Entsättigung der tolerierte Umgebungsdruck kleiner oder gleich dem Umgebungsdruck auf der nächst niedriegeren Dekostufe ist.
Das Programm CheckDive 3M (Trimix) arbeitet nach diesem Prinzip.
Hier wird 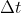 per Voreinstellung mit 1 min. angesetzt, da das die minimale Zeit ist, die auf einer Dekostufe verblieben werden soll. Allerdings können per Checkbox auch kleinere Zeiteinheiten ausgewählt werden. Hier steigt der Rechenaufwand allerdings proportional. per Voreinstellung mit 1 min. angesetzt, da das die minimale Zeit ist, die auf einer Dekostufe verblieben werden soll. Allerdings können per Checkbox auch kleinere Zeiteinheiten ausgewählt werden. Hier steigt der Rechenaufwand allerdings proportional.
|


